As Árvores B são estruturas de dados fundamentais na ciência da computação, especialmente no contexto de sistemas de gerenciamento de bancos de dados (SGBDs). Elas desempenham um papel crucial na indexação eficiente de grandes volumes de dados, permitindo operações de busca, inserção e exclusão em tempo logarítmico. Neste artigo, mergulharemos profundamente na implementação e otimização de Árvores B para indexação de bancos de dados, explorando técnicas avançadas e considerações de desempenho.
Fundamentos das Árvores B
Antes de nos aprofundarmos nas técnicas de implementação e otimização, é essencial compreender os princípios fundamentais das Árvores B.
Definição e Propriedades
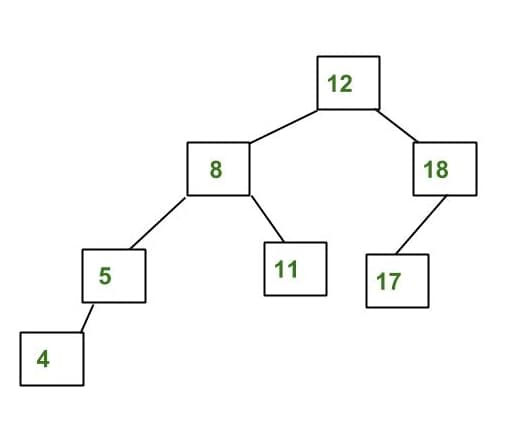
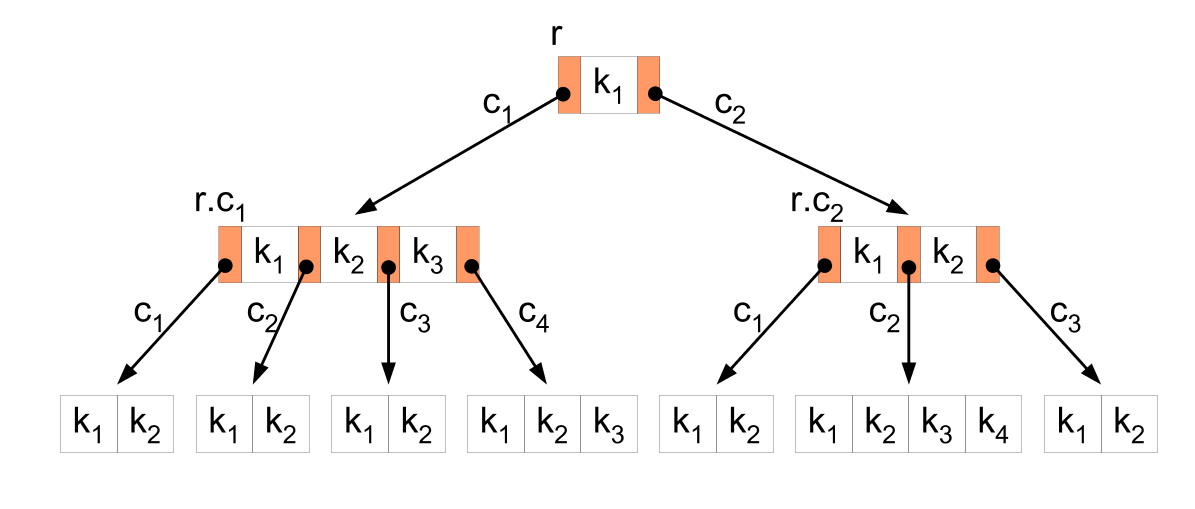
Uma Árvore B é uma estrutura de dados em árvore balanceada, projetada para armazenar e recuperar grandes quantidades de dados de forma eficiente. Algumas propriedades importantes das Árvores B incluem:
Todos os nós folha estão no mesmo nível.
Cada nó interno (exceto a raiz) tem pelo menos ⌈m/2⌉ filhos, onde m é a ordem da árvore.
Cada nó interno (exceto a raiz) contém pelo menos ⌈m/2⌉ - 1 chaves.
A raiz tem pelo menos dois filhos, a menos que seja uma folha.
Um nó com k chaves tem k+1 filhos.
As chaves dentro de um nó estão ordenadas.
Operações Básicas
As operações fundamentais em uma Árvore B são:
Busca
Inserção
Exclusão
Vamos implementar essas operações em Python para ilustrar seu funcionamento.
class BTreeNode:
def __init__(self, leaf=False):
self.leaf = leaf
self.keys = []
self.children = []
class BTree:
def __init__(self, t):
self.root = BTreeNode(True)
self.t = t # Grau mínimo
def search(self, k, x=None):
if x is None:
x = self.root
i = 0
while i < len(x.keys) and k > x.keys[i]:
i += 1
if i < len(x.keys) and k == x.keys[i]:
return (x, i)
elif x.leaf:
return None
else:
return self.search(k, x.children[i])
def insert(self, k):
root = self.root
if len(root.keys) == (2 * self.t) - 1:
new_root = BTreeNode()
self.root = new_root
new_root.children.insert(0, root)
self._split_child(new_root, 0)
self._insert_non_full(new_root, k)
else:
self._insert_non_full(root, k)
def _insert_non_full(self, x, k):
i = len(x.keys) - 1
if x.leaf:
x.keys.append(None)
while i >= 0 and k < x.keys[i]:
x.keys[i + 1] = x.keys[i]
i -= 1
x.keys[i + 1] = k
else:
while i >= 0 and k < x.keys[i]:
i -= 1
i += 1
if len(x.children[i].keys) == (2 * self.t) - 1:
self._split_child(x, i)
if k > x.keys[i]:
i += 1
self._insert_non_full(x.children[i], k)
def _split_child(self, x, i):
t = self.t
y = x.children[i]
z = BTreeNode(y.leaf)
x.children.insert(i + 1, z)
x.keys.insert(i, y.keys[t - 1])
z.keys = y.keys[t:]
y.keys = y.keys[:t - 1]
if not y.leaf:
z.children = y.children[t:]
y.children = y.children[:t]
Esta implementação básica fornece uma base sólida para entender como as Árvores B funcionam. No entanto, para uso em sistemas de bancos de dados reais, precisamos considerar otimizações e técnicas avançadas.
Técnicas Avançadas de Implementação
Compressão de Nós
Uma técnica comum para otimizar o uso de memória em Árvores B é a compressão de nós. Isso envolve armazenar as chaves e ponteiros de forma mais eficiente, reduzindo o espaço necessário para cada nó.
class CompressedBTreeNode:
def __init__(self, leaf=False):
self.leaf = leaf
self.data = bytearray() # Armazena chaves e ponteiros de forma compacta
self.num_keys = 0
def insert_key(self, key, index):
# Implementação da inserção de chave no formato comprimido
pass
def get_key(self, index):
# Implementação da recuperação de chave do formato comprimido
pass
Buffering e Caching
Para melhorar o desempenho em operações de I/O, podemos implementar um sistema de buffering e caching. Isso envolve manter os nós frequentemente acessados na memória principal.
class BTreeBuffer:
def __init__(self, capacity):
self.capacity = capacity
self.buffer = {}
self.lru = []
def get(self, node_id):
if node_id in self.buffer:
self.lru.remove(node_id)
self.lru.append(node_id)
return self.buffer[node_id]
return None
def put(self, node_id, node):
if len(self.buffer) >= self.capacity:
oldest = self.lru.pop(0)
del self.buffer[oldest]
self.buffer[node_id] = node
self.lru.append(node_id)
Otimização para Sistemas de Bancos de Dados
Adaptação para Armazenamento em Disco
Em sistemas de bancos de dados reais, as Árvores B são frequentemente armazenadas em disco. Isso requer adaptações na implementação para lidar eficientemente com operações de I/O.
class DiskBTree:
def __init__(self, filename, order):
self.filename = filename
self.order = order
self.root_address = 0
self.free_list = []
def read_node(self, address):
# Lê um nó do disco
pass
def write_node(self, node, address=None):
# Escreve um nó no disco
pass
def allocate_node(self):
# Aloca espaço para um novo nó no disco
pass
def free_node(self, address):
# Libera o espaço de um nó no disco
pass
Otimização de Consultas
Para melhorar o desempenho de consultas em bancos de dados, podemos implementar técnicas como:
Prefetching: Carregar nós adjacentes antecipadamente.
Bulk loading: Construir a árvore de forma eficiente para grandes conjuntos de dados iniciais.
Compressão de índices: Reduzir o tamanho dos índices para melhorar a eficiência de cache.
class OptimizedBTree(DiskBTree):
def prefetch(self, node):
# Implementação de prefetching
pass
def bulk_load(self, data):
# Implementação de bulk loading
pass
def compress_index(self):
# Implementação de compressão de índices
pass
Considerações de Concorrência
Em ambientes de banco de dados com múltiplos usuários, é crucial implementar mecanismos de concorrência para garantir a integridade dos dados.
Bloqueio de Granularidade Fina
Implementar bloqueios de granularidade fina permite que múltiplas transações acessem diferentes partes da árvore simultaneamente.
class ConcurrentBTree(OptimizedBTree):
def __init__(self, filename, order):
super().__init__(filename, order)
self.locks = {}
def acquire_lock(self, node_id, mode='shared'):
# Implementação de aquisição de bloqueio
pass
def release_lock(self, node_id):
# Implementação de liberação de bloqueio
pass
def insert(self, key, value):
# Implementação de inserção com controle de concorrência
pass
def delete(self, key):
# Implementação de exclusão com controle de concorrência
pass
Técnicas de Latch-Free
Para sistemas de alto desempenho, podemos considerar implementações latch-free das Árvores B, que eliminam a necessidade de bloqueios explícitos.
class LatchFreeBTree:
def __init__(self):
self.root = AtomicReference(BTreeNode())
def insert(self, key, value):
while True:
root = self.root.get()
new_root = self._insert_recursive(root, key, value)
if new_root is root:
return
if self.root.compare_and_set(root, new_root):
return
def _insert_recursive(self, node, key, value):
# Implementação recursiva da inserção latch-free
pass
Análise de Desempenho e Otimização
Para garantir que nossa implementação de Árvore B seja eficiente, devemos realizar análises de desempenho e otimizações contínuas.
Benchmarking
Implementar benchmarks para medir o desempenho das operações da Árvore B em diferentes cenários.
def benchmark_btree(btree, num_operations):
import time
import random
start_time = time.time()
for _ in range(num_operations):
operation = random.choice(['insert', 'search', 'delete'])
key = random.randint(1, 1000000)
if operation == 'insert':
btree.insert(key, f"value_{key}")
elif operation == 'search':
btree.search(key)
else:
btree.delete(key)
end_time = time.time()
return end_time - start_time
Profiling
Usar ferramentas de profiling para identificar gargalos de desempenho na implementação.
import cProfile
def profile_btree_operations():
btree = BTree(3)
cProfile.runctx('benchmark_btree(btree, 100000)', globals(), locals(), 'btree_profile.stats')
# Analisar os resultados do profiling
# pstats.Stats('btree_profile.stats').sort_stats('cumulative').print_stats()
Conclusão
A implementação e otimização de Árvores B para indexação eficiente de bancos de dados é um tópico complexo e crucial no desenvolvimento de sistemas de gerenciamento de bancos de dados de alto desempenho. Neste artigo, exploramos os fundamentos das Árvores B, técnicas avançadas de implementação, otimizações específicas para sistemas de bancos de dados e considerações de concorrência.
Ao aplicar essas técnicas e otimizações, podemos criar estruturas de indexação altamente eficientes que permitem operações rápidas de busca, inserção e exclusão em grandes volumes de dados. No entanto, é importante lembrar que a otimização é um processo contínuo, e as técnicas específicas podem variar dependendo dos requisitos e características do sistema em questão.
Como desenvolvedores e arquitetos de sistemas de bancos de dados, devemos sempre buscar o equilíbrio entre eficiência, escalabilidade e manutenibilidade em nossas implementações de estruturas de dados. As Árvores B, quando implementadas e otimizadas corretamente, continuam sendo uma ferramenta poderosa no arsenal de técnicas para construção de sistemas de gerenciamento de bancos de dados robustos e eficientes.