As árvores de segmentos (Segment Trees) são estruturas de dados poderosas e versáteis que permitem realizar consultas e atualizações eficientes em intervalos de dados. Essa estrutura é amplamente utilizada em programação competitiva e em cenários do mundo real onde é necessário processar grandes conjuntos de dados de forma rápida e eficiente.
Neste artigo, vamos mergulhar fundo no mundo das árvores de segmentos, explorando sua implementação, otimização e aplicações práticas. Vamos além dos conceitos básicos, focando em técnicas avançadas que permitirão que você aproveite todo o potencial dessa estrutura de dados.
Fundamentos das Árvores de Segmentos
Antes de nos aprofundarmos nas técnicas avançadas, vamos revisar brevemente os conceitos fundamentais das árvores de segmentos.
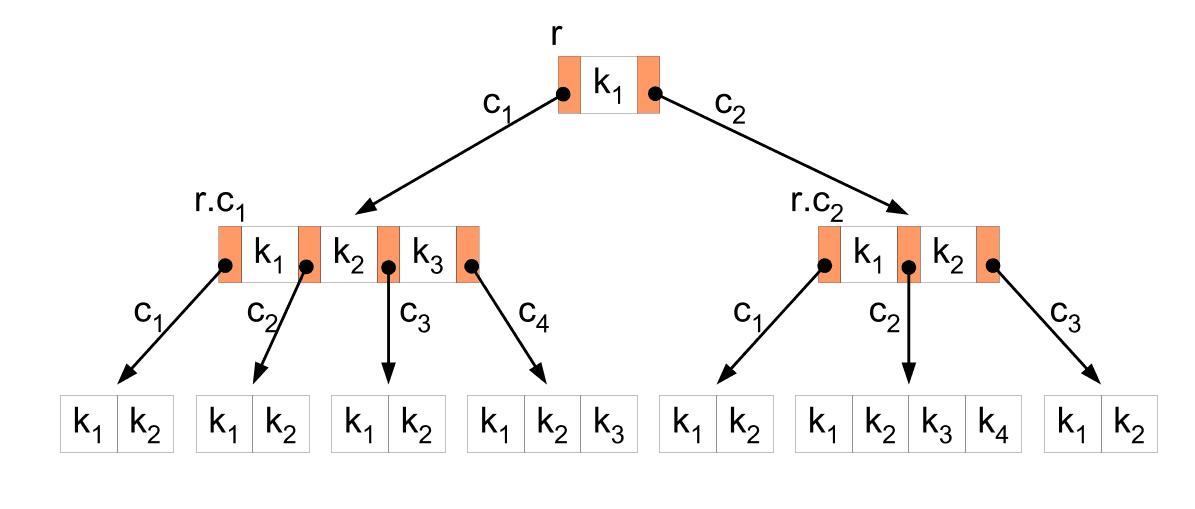
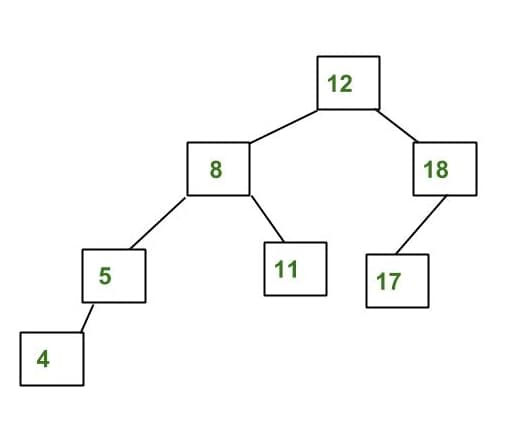
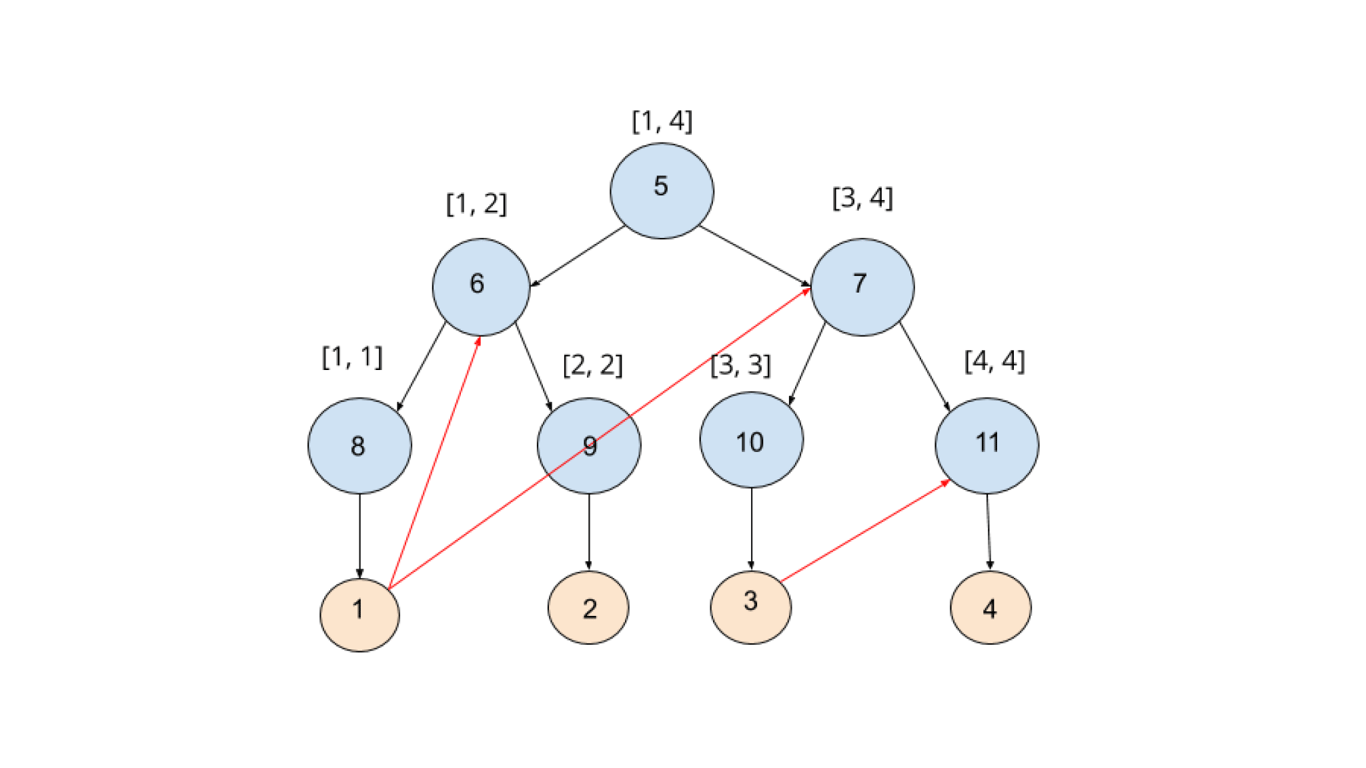
Uma árvore de segmentos é uma estrutura de dados em forma de árvore binária que permite realizar operações de consulta e atualização em intervalos de um array em tempo O(log n), onde n é o tamanho do array. Cada nó da árvore representa um intervalo do array original, com o nó raiz representando todo o array e os nós folha representando elementos individuais.
A estrutura básica de um nó da árvore de segmentos pode ser definida da seguinte forma:
struct SegmentTreeNode {
int start, end;
long long sum;
SegmentTreeNode *left, *right;
SegmentTreeNode(int start, int end) : start(start), end(end), sum(0), left(nullptr), right(nullptr) {}
};
Implementação Eficiente
Agora, vamos implementar as operações básicas de uma árvore de segmentos de forma eficiente.
Construção da Árvore
A construção da árvore é feita de forma recursiva, dividindo o intervalo ao meio e construindo os nós filhos:
SegmentTreeNode* buildTree(vector<int>& nums, int start, int end) {
if (start > end) return nullptr;
SegmentTreeNode* root = new SegmentTreeNode(start, end);
if (start == end) {
root->sum = nums[start];
} else {
int mid = start + (end - start) / 2;
root->left = buildTree(nums, start, mid);
root->right = buildTree(nums, mid + 1, end);
root->sum = (root->left ? root->left->sum : 0) + (root->right ? root->right->sum : 0);
}
return root;
}
Consulta em Intervalo
A operação de consulta em intervalo é implementada de forma recursiva, verificando a sobreposição entre o intervalo consultado e o intervalo do nó atual:
long long queryRange(SegmentTreeNode* root, int start, int end) {
if (!root || start > root->end || end < root->start) return 0;
if (start <= root->start && end >= root->end) return root->sum;
return queryRange(root->left, start, end) + queryRange(root->right, start, end);
}
Atualização de Elemento
A atualização de um elemento é feita percorrendo a árvore até o nó folha correspondente e atualizando os valores dos nós ancestrais:
void updateElement(SegmentTreeNode* root, int index, int value) {
if (!root || index < root->start || index > root->end) return;
if (root->start == root->end) {
root->sum = value;
return;
}
int mid = root->start + (root->end - root->start) / 2;
if (index <= mid) {
updateElement(root->left, index, value);
} else {
updateElement(root->right, index, value);
}
root->sum = (root->left ? root->left->sum : 0) + (root->right ? root->right->sum : 0);
}
Otimização e Técnicas Avançadas
Agora que temos uma implementação básica, vamos explorar algumas técnicas avançadas para otimizar nossa árvore de segmentos.
Lazy Propagation
A técnica de lazy propagation é crucial para melhorar a eficiência das atualizações em intervalos. Em vez de atualizar imediatamente todos os nós afetados, adiamos as atualizações até que seja necessário.
Vamos modificar nossa estrutura de nó para incluir um campo de lazy:
struct SegmentTreeNode {
int start, end;
long long sum, lazy;
SegmentTreeNode *left, *right;
SegmentTreeNode(int start, int end) : start(start), end(end), sum(0), lazy(0), left(nullptr), right(nullptr) {}
};
Agora, implementamos a função de propagação lazy:
void pushDown(SegmentTreeNode* node) {
if (!node || !node->lazy) return;
if (node->left) {
node->left->lazy += node->lazy;
node->left->sum += node->lazy * (node->left->end - node->left->start + 1);
}
if (node->right) {
node->right->lazy += node->lazy;
node->right->sum += node->lazy * (node->right->end - node->right->start + 1);
}
node->lazy = 0;
}
E modificamos nossas funções de consulta e atualização para usar a propagação lazy:
long long queryRange(SegmentTreeNode* root, int start, int end) {
if (!root || start > root->end || end < root->start) return 0;
if (start <= root->start && end >= root->end) {
return root->sum;
}
pushDown(root);
return queryRange(root->left, start, end) + queryRange(root->right, start, end);
}
void updateRange(SegmentTreeNode* root, int start, int end, int value) {
if (!root || start > root->end || end < root->start) return;
if (start <= root->start && end >= root->end) {
root->sum += value * (root->end - root->start + 1);
root->lazy += value;
return;
}
pushDown(root);
updateRange(root->left, start, end, value);
updateRange(root->right, start, end, value);
root->sum = (root->left ? root->left->sum : 0) + (root->right ? root->right->sum : 0);
}
Compressão de Coordenadas
Quando lidamos com intervalos muito grandes ou esparsos, podemos usar a técnica de compressão de coordenadas para reduzir o espaço necessário para a árvore de segmentos.
vector<int> compressCoordinates(vector<pair<int, int>>& intervals) {
set<int> coords;
for (auto& interval : intervals) {
coords.insert(interval.first);
coords.insert(interval.second);
}
vector<int> compressed(coords.begin(), coords.end());
sort(compressed.begin(), compressed.end());
unordered_map<int, int> coordMap;
for (int i = 0; i < compressed.size(); i++) {
coordMap[compressed[i]] = i;
}
for (auto& interval : intervals) {
interval.first = coordMap[interval.first];
interval.second = coordMap[interval.second];
}
return compressed;
}
Persistência
Para problemas que exigem consultas em versões anteriores da árvore, podemos implementar uma árvore de segmentos persistente:
struct PersistentSegmentTreeNode {
long long sum;
PersistentSegmentTreeNode *left, *right;
PersistentSegmentTreeNode(long long sum) : sum(sum), left(nullptr), right(nullptr) {}
PersistentSegmentTreeNode(PersistentSegmentTreeNode* node) : sum(node->sum), left(node->left), right(node->right) {}
};
PersistentSegmentTreeNode* updatePersistent(PersistentSegmentTreeNode* node, int start, int end, int index, int value) {
if (start == end) {
PersistentSegmentTreeNode* newNode = new PersistentSegmentTreeNode(node);
newNode->sum = value;
return newNode;
}
PersistentSegmentTreeNode* newNode = new PersistentSegmentTreeNode(node);
int mid = start + (end - start) / 2;
if (index <= mid) {
newNode->left = updatePersistent(node->left, start, mid, index, value);
} else {
newNode->right = updatePersistent(node->right, mid + 1, end, index, value);
}
newNode->sum = newNode->left->sum + newNode->right->sum;
return newNode;
}
Aplicações Práticas
As árvores de segmentos têm uma ampla gama de aplicações práticas. Vamos explorar alguns cenários onde essa estrutura de dados pode ser extremamente útil.
Problemas de Programação Competitiva
As árvores de segmentos são frequentemente usadas em problemas de programação competitiva que envolvem consultas e atualizações em intervalos. Por exemplo, considere o seguinte problema:
"Dado um array de n inteiros, realize m operações. Cada operação pode ser uma consulta da soma em um intervalo [l, r] ou uma atualização do valor de um elemento específico."
A árvore de segmentos permite resolver esse problema com complexidade O(log n) por operação, tornando-a ideal para lidar com grandes conjuntos de dados e muitas operações.
Análise de Dados em Tempo Real
Em cenários de análise de dados em tempo real, onde grandes volumes de dados estão sendo constantemente atualizados e consultados, as árvores de segmentos podem oferecer um desempenho superior.
Por exemplo, em um sistema de monitoramento de tráfego de rede, podemos usar uma árvore de segmentos para manter estatísticas sobre o uso de largura de banda em diferentes intervalos de tempo, permitindo consultas rápidas e atualizações eficientes.
Processamento de Imagens
No processamento de imagens, as árvores de segmentos podem ser usadas para realizar operações eficientes em regiões retangulares de uma imagem. Por exemplo, podemos usar uma árvore de segmentos 2D para calcular rapidamente a soma dos valores de pixel em uma região específica ou para aplicar filtros a áreas selecionadas da imagem.
Conclusão
As árvores de segmentos são uma ferramenta poderosa no arsenal de qualquer programador avançado. Sua capacidade de realizar consultas e atualizações eficientes em intervalos as torna indispensáveis em muitos cenários de programação competitiva e desenvolvimento de software de alto desempenho.
Neste artigo, exploramos a implementação eficiente de árvores de segmentos, técnicas avançadas de otimização como lazy propagation e compressão de coordenadas, e discutimos aplicações práticas dessa estrutura de dados.
Ao dominar as árvores de segmentos, você estará bem equipado para enfrentar uma ampla gama de problemas complexos que envolvem operações em intervalos. Continue praticando e explorando novas formas de aplicar essa versátil estrutura de dados em seus projetos e desafios de programação.
Lembre-se, a verdadeira maestria vem não apenas da compreensão dos conceitos, mas também da aplicação prática e da experimentação contínua. Desafie-se a implementar variações das árvores de segmentos e a usá-las em problemas do mundo real para realmente solidificar seu entendimento e habilidades.