As árvores de busca binária auto-balanceadas são estruturas de dados fundamentais na ciência da computação, oferecendo um equilíbrio crucial entre eficiência de busca e manutenção da estrutura. Duas das implementações mais populares são as árvores AVL e as árvores Rubro-Negras. Neste artigo, mergulharemos profundamente na análise de complexidade de tempo e espaço dessas estruturas, explorando suas diferenças teóricas e práticas, bem como suas aplicações no mundo real.
Fundamentos das Árvores de Busca Binária Auto-balanceadas
Antes de nos aprofundarmos nas especificidades das árvores AVL e Rubro-Negras, é importante revisitar os conceitos fundamentais das árvores de busca binária auto-balanceadas.
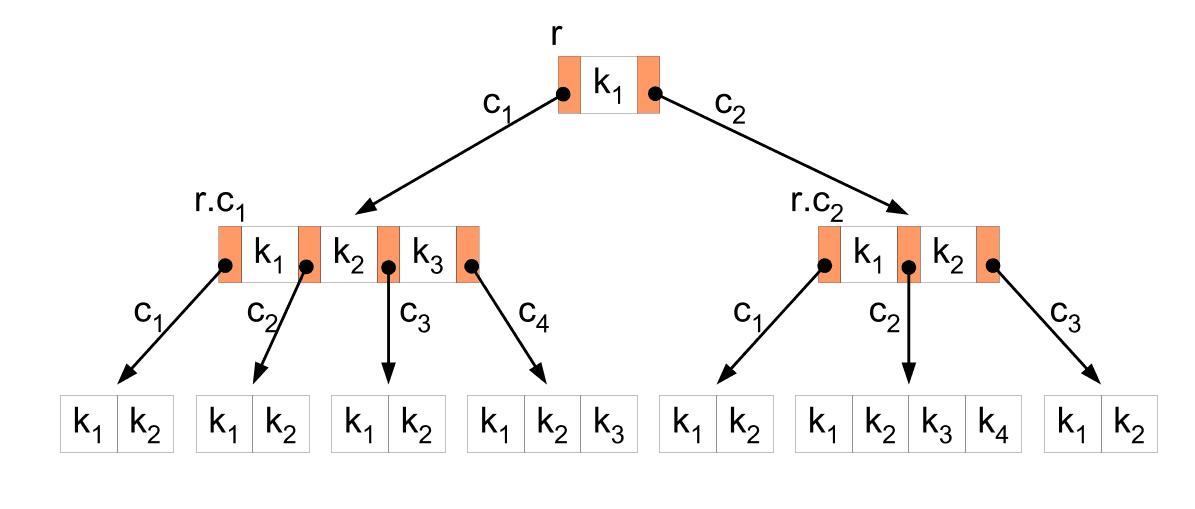
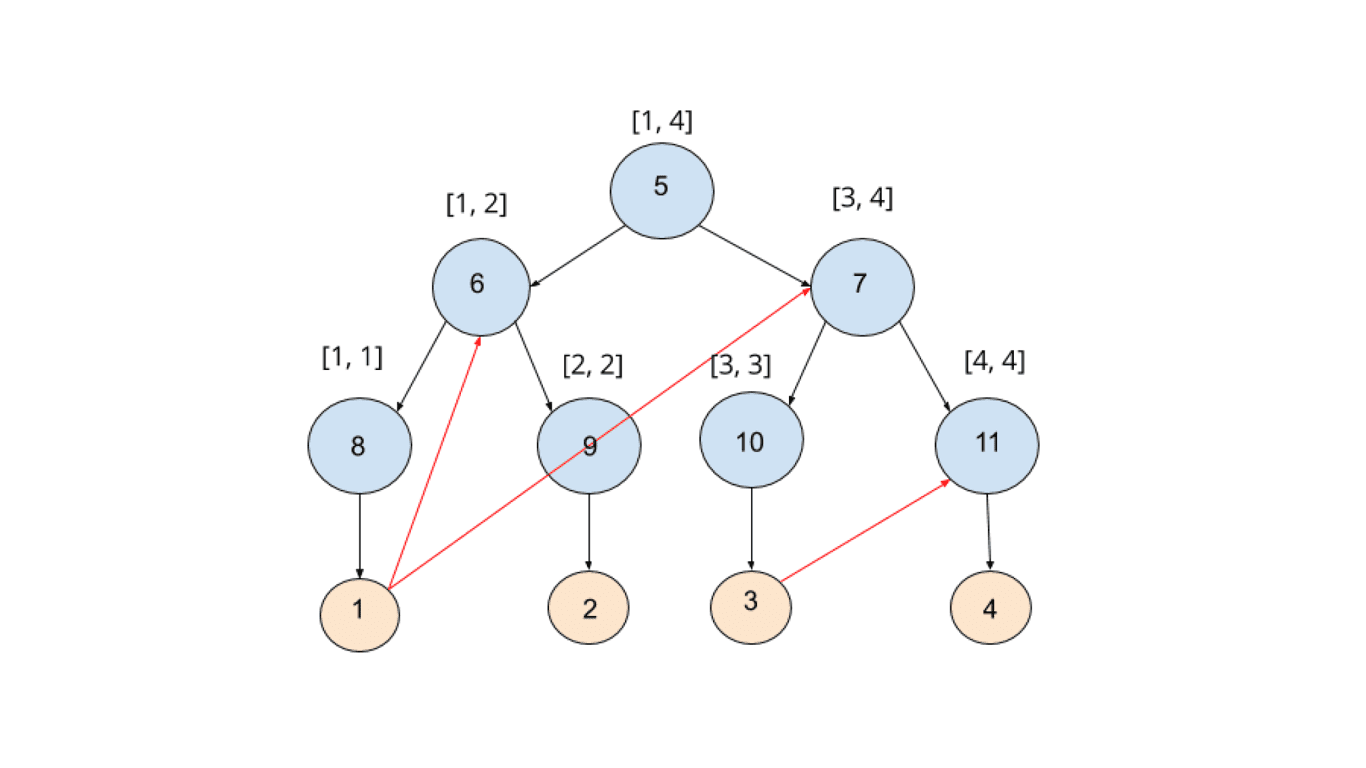
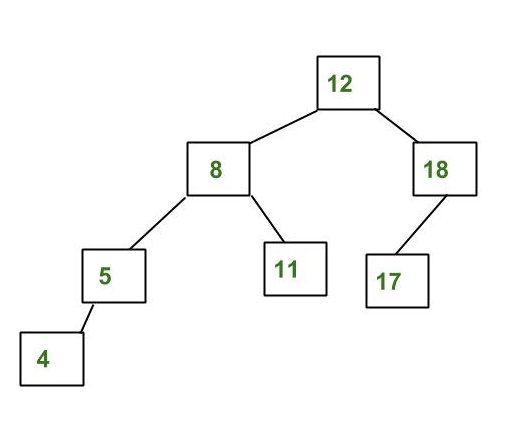
Uma árvore de busca binária é uma estrutura de dados em que cada nó tem no máximo dois filhos, comumente chamados de filho esquerdo e filho direito. A propriedade chave é que, para qualquer nó, todos os elementos na subárvore esquerda são menores que o nó, e todos os elementos na subárvore direita são maiores.
O problema com árvores de busca binária simples é que elas podem se degenerar em listas ligadas se os elementos forem inseridos em ordem crescente ou decrescente, levando a um desempenho de busca de O(n) no pior caso, onde n é o número de elementos.
As árvores auto-balanceadas resolvem esse problema mantendo a árvore balanceada, garantindo uma altura logarítmica e, consequentemente, operações de busca, inserção e remoção em O(log n) no pior caso.
Árvores AVL: Análise de Complexidade
As árvores AVL, nomeadas após seus inventores Adelson-Velsky e Landis, foram a primeira estrutura de dados de árvore de busca binária auto-balanceada a ser inventada.
Propriedades de Balanceamento
Uma árvore AVL mantém a seguinte propriedade de balanceamento:
Para cada nó, a diferença de altura entre as subárvores esquerda e direita (o fator de balanceamento) deve ser no máximo 1.
Complexidade de Tempo
Busca: O(log n)
Inserção: O(log n)
Remoção: O(log n)
A busca em uma árvore AVL é idêntica à busca em uma árvore de busca binária regular. A complexidade logarítmica é garantida pela propriedade de balanceamento.
As operações de inserção e remoção podem requerer rebalanceamento da árvore. Isso é feito através de rotações, que são operações de tempo constante. No pior caso, pode ser necessário realizar O(log n) rotações ao longo do caminho da raiz até o ponto de inserção/remoção.
Complexidade de Espaço
A complexidade de espaço de uma árvore AVL é O(n), onde n é o número de elementos. Cada nó requer espaço adicional para armazenar o fator de balanceamento ou a altura.
Implementação em Python
Vamos examinar uma implementação básica de uma árvore AVL em Python:
class AVLNode:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
self.height = 1
class AVLTree:
def __init__(self):
self.root = None
def height(self, node):
if not node:
return 0
return node.height
def balance_factor(self, node):
if not node:
return 0
return self.height(node.left) - self.height(node.right)
def update_height(self, node):
if not node:
return
node.height = 1 + max(self.height(node.left), self.height(node.right))
def rotate_right(self, y):
x = y.left
T2 = x.right
x.right = y
y.left = T2
self.update_height(y)
self.update_height(x)
return x
def rotate_left(self, x):
y = x.right
T2 = y.left
y.left = x
x.right = T2
self.update_height(x)
self.update_height(y)
return y
def insert(self, root, key):
if not root:
return AVLNode(key)
if key < root.key:
root.left = self.insert(root.left, key)
else:
root.right = self.insert(root.right, key)
self.update_height(root)
balance = self.balance_factor(root)
# Casos de balanceamento
if balance > 1:
if key < root.left.key:
return self.rotate_right(root)
else:
root.left = self.rotate_left(root.left)
return self.rotate_right(root)
if balance < -1:
if key > root.right.key:
return self.rotate_left(root)
else:
root.right = self.rotate_right(root.right)
return self.rotate_left(root)
return root
def insert_key(self, key):
self.root = self.insert(self.root, key)
Esta implementação demonstra as operações fundamentais de uma árvore AVL, incluindo as rotações necessárias para manter o balanceamento.
Árvores Rubro-Negras: Análise de Complexidade
As árvores Rubro-Negras são outra forma popular de árvore de busca binária auto-balanceada, inventadas por Rudolf Bayer em 1972.
Propriedades de Balanceamento
Uma árvore Rubro-Negra mantém as seguintes propriedades:
Cada nó é vermelho ou preto.
A raiz é sempre preta.
Todas as folhas (NIL) são pretas.
Se um nó é vermelho, então ambos os seus filhos são pretos.
Para cada nó, todos os caminhos do nó até as folhas descendentes contêm o mesmo número de nós pretos.
Complexidade de Tempo
Busca: O(log n)
Inserção: O(log n)
Remoção: O(log n)
Assim como nas árvores AVL, a busca em uma árvore Rubro-Negra é idêntica à busca em uma árvore de busca binária regular.
As operações de inserção e remoção podem requerer recoloração e rotações para manter as propriedades da árvore Rubro-Negra. No entanto, o número de rotações é limitado a um máximo de três para inserção e três para remoção.
Complexidade de Espaço
A complexidade de espaço de uma árvore Rubro-Negra é O(n), onde n é o número de elementos. Cada nó requer um bit adicional para armazenar a cor.
Implementação em Python
Vamos examinar uma implementação básica de uma árvore Rubro-Negra em Python:
class Color:
RED = 1
BLACK = 2
class RBNode:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
self.parent = None
self.color = Color.RED
class RBTree:
def __init__(self):
self.NIL = RBNode(0)
self.NIL.color = Color.BLACK
self.NIL.left = None
self.NIL.right = None
self.root = self.NIL
def insert(self, key):
node = RBNode(key)
node.left = self.NIL
node.right = self.NIL
y = None
x = self.root
while x != self.NIL:
y = x
if node.key < x.key:
x = x.left
else:
x = x.right
node.parent = y
if y == None:
self.root = node
elif node.key < y.key:
y.left = node
else:
y.right = node
self.fix_insert(node)
def fix_insert(self, k):
while k.parent and k.parent.color == Color.RED:
if k.parent == k.parent.parent.right:
u = k.parent.parent.left
if u.color == Color.RED:
u.color = Color.BLACK
k.parent.color = Color.BLACK
k.parent.parent.color = Color.RED
k = k.parent.parent
else:
if k == k.parent.left:
k = k.parent
self.rotate_right(k)
k.parent.color = Color.BLACK
k.parent.parent.color = Color.RED
self.rotate_left(k.parent.parent)
else:
u = k.parent.parent.right
if u.color == Color.RED:
u.color = Color.BLACK
k.parent.color = Color.BLACK
k.parent.parent.color = Color.RED
k = k.parent.parent
else:
if k == k.parent.right:
k = k.parent
self.rotate_left(k)
k.parent.color = Color.BLACK
k.parent.parent.color = Color.RED
self.rotate_right(k.parent.parent)
if k == self.root:
break
self.root.color = Color.BLACK
def rotate_left(self, x):
y = x.right
x.right = y.left
if y.left != self.NIL:
y.left.parent = x
y.parent = x.parent
if x.parent == None:
self.root = y
elif x == x.parent.left:
x.parent.left = y
else:
x.parent.right = y
y.left = x
x.parent = y
def rotate_right(self, x):
y = x.left
x.left = y.right
if y.right != self.NIL:
y.right.parent = x
y.parent = x.parent
if x.parent == None:
self.root = y
elif x == x.parent.right:
x.parent.right = y
else:
x.parent.left = y
y.right = x
x.parent = y
Esta implementação demonstra as operações fundamentais de uma árvore Rubro-Negra, incluindo as rotações e recolorações necessárias para manter as propriedades da árvore.
Comparação de Desempenho: AVL vs. Rubro-Negra
Agora que examinamos as propriedades e implementações de ambas as estruturas, vamos comparar seu desempenho em diferentes cenários.
Operações de Busca
Tanto as árvores AVL quanto as Rubro-Negras garantem operações de busca em O(log n). No entanto, as árvores AVL tendem a ser mais balanceadas, o que pode resultar em buscas ligeiramente mais rápidas na prática.
Operações de Inserção e Remoção
As árvores Rubro-Negras geralmente têm um desempenho melhor em operações de inserção e remoção. Isso ocorre porque elas requerem menos rotações em média. As árvores AVL, sendo mais estritamente balanceadas, podem exigir mais rotações para manter o balanceamento após inserções ou remoções.
Uso de Memória
As árvores Rubro-Negras têm uma ligeira vantagem em termos de uso de memória. Elas requerem apenas um bit extra por nó para armazenar a cor, enquanto as árvores AVL geralmente armazenam um fator de balanceamento ou altura, que pode requerer um inteiro.
Aplicações no Mundo Real
A escolha entre árvores AVL e Rubro-Negras depende muito do caso de uso específico. Vamos examinar algumas aplicações do mundo real:
Sistemas de Arquivos
Muitos sistemas de arquivos, como o ext4 usado em sistemas Linux, utilizam árvores Rubro-Negras para gerenciar metadados de arquivos. A eficiência das operações de inserção e remoção das árvores Rubro-Negras é particularmente útil neste contexto, onde arquivos são frequentemente criados e excluídos.
Bancos de Dados
Sistemas de gerenciamento de banco de dados frequentemente utilizam árvores B+ para índices, que são uma generalização das árvores de busca binária balanceadas. No entanto, para índices menores ou em memória, tanto árvores AVL quanto Rubro-Negras podem ser usadas. O PostgreSQL, por exemplo, usa uma variante de árvore Rubro-Negra chamada GiST (Generalized Search Tree) para alguns de seus índices.
Compiladores e Interpretadores
Compiladores e interpretadores frequentemente usam árvores de busca binária balanceadas para tabelas de símbolos. As árvores AVL podem ser preferidas neste contexto devido à sua busca ligeiramente mais rápida, especialmente se as operações de leitura são muito mais frequentes que as de escrita.
Algoritmos de Roteamento
Em redes de computadores, algoritmos de roteamento podem usar árvores de busca binária balanceadas para armazenar e buscar informações de roteamento. A escolha entre AVL e Rubro-Negra pode depender da frequência relativa de atualizações de rota versus consultas de rota.
Conclusão
Tanto as árvores AVL quanto as Rubro-Negras são estruturas de dados poderosas que oferecem excelente desempenho para operações de busca, inserção e remoção. A escolha entre elas depende das características específicas da aplicação.
As árvores AVL são ideais para cenários onde as operações de leitura são significativamente mais frequentes que as de escrita, e onde o balanceamento estrito pode oferecer benefícios tangíveis.
As árvores Rubro-Negras, por outro lado, são mais adequadas para aplicações com uma mistura mais equilibrada de operações de leitura e escrita, ou onde as operações de inserção e remoção são particularmente frequentes.
Em última análise, a decisão entre AVL e Rubro-Negra muitas vezes vem down para benchmarks específicos da aplicação. Em muitos casos, a diferença de desempenho pode ser mínima, e outros fatores, como a familiaridade da equipe com uma estrutura particular ou a disponibilidade de implementações testadas e otimizadas, podem ser mais importantes na decisão final.
Independentemente da escolha, o entendimento profundo dessas estruturas de dados e suas complexidades é crucial para qualquer programador sério, permitindo decisões informadas de design e otimização em uma ampla gama de aplicações do mundo real.