A compressão de dados sem perdas é um campo crucial da ciência da computação, especialmente em uma era dominada por big data e transmissões em tempo real. Este artigo se propõe a analisar em profundidade três abordagens fundamentais para compressão de dados sem perdas: o algoritmo de Huffman, o LZ77 e os algoritmos baseados em dicionário. Vamos explorar suas estruturas, eficiência e aplicabilidade em cenários modernos de processamento de dados.
1. Algoritmo de Huffman
1.1 Fundamentos Teóricos
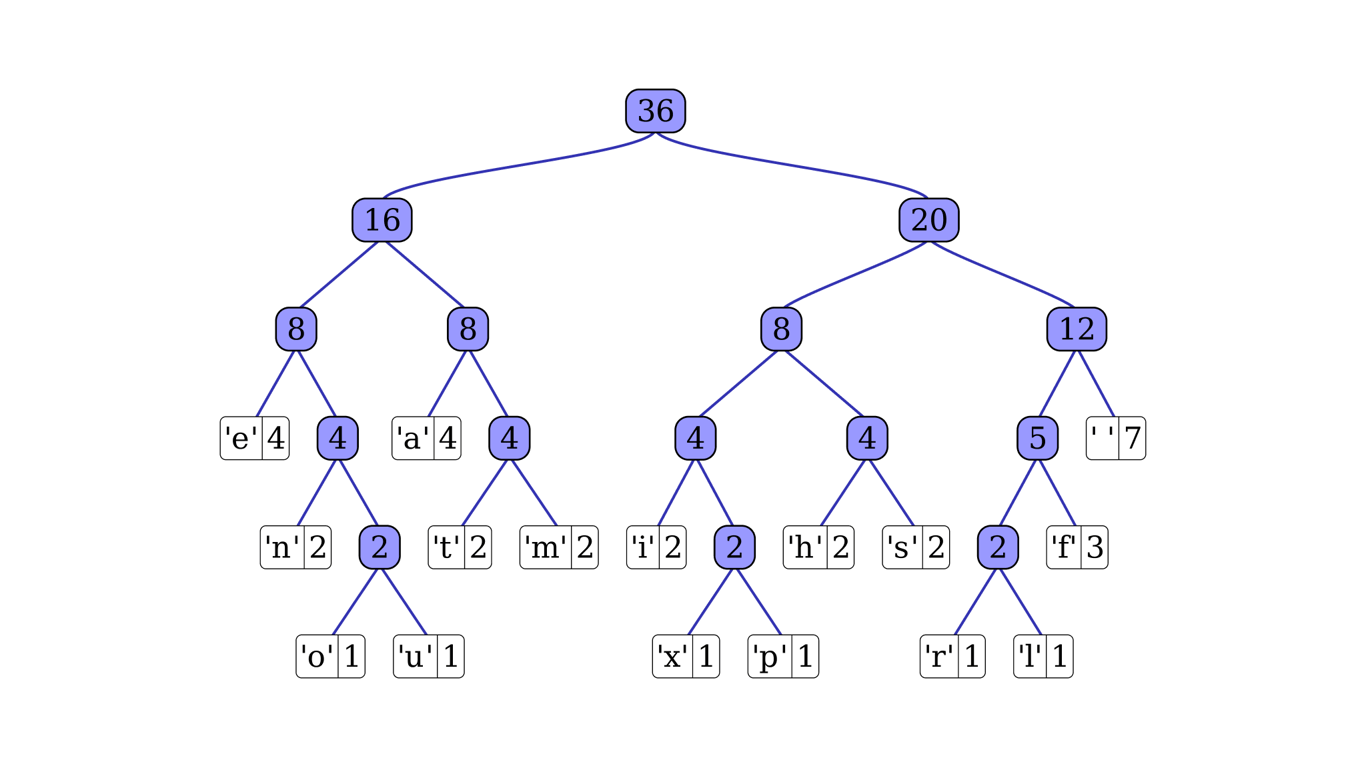
O algoritmo de Huffman, desenvolvido por David A. Huffman em 1952, é um método de compressão que utiliza códigos de comprimento variável para representar símbolos. A ideia central é atribuir códigos mais curtos a símbolos mais frequentes e códigos mais longos a símbolos menos frequentes.
1.2 Implementação
Vamos examinar uma implementação básica do algoritmo de Huffman em Python:
import heapq
from collections import defaultdict
class HuffmanNode:
def __init__(self, char, freq):
self.char = char
self.freq = freq
self.left = None
self.right = None
def __lt__(self, other):
return self.freq < other.freq
def build_huffman_tree(text):
frequency = defaultdict(int)
for char in text:
frequency[char] += 1
heap = [HuffmanNode(char, freq) for char, freq in frequency.items()]
heapq.heapify(heap)
while len(heap) > 1:
left = heapq.heappop(heap)
right = heapq.heappop(heap)
merged = HuffmanNode(None, left.freq + right.freq)
merged.left = left
merged.right = right
heapq.heappush(heap, merged)
return heap[0]
def build_huffman_codes(node, current_code="", codes={}):
if node is None:
return
if node.char is not None:
codes[node.char] = current_code
return
build_huffman_codes(node.left, current_code + "0", codes)
build_huffman_codes(node.right, current_code + "1", codes)
return codes
def huffman_encode(text):
root = build_huffman_tree(text)
codes = build_huffman_codes(root)
encoded_text = "".join(codes[char] for char in text)
return encoded_text, codes
# Exemplo de uso
text = "este é um exemplo de texto para compressão"
encoded_text, codes = huffman_encode(text)
print("Texto codificado:", encoded_text)
print("Códigos Huffman:", codes)
1.3 Análise de Eficiência
O algoritmo de Huffman tem uma complexidade de tempo de O(n log n), onde n é o número de símbolos únicos no texto. Isso se deve principalmente à construção da árvore de Huffman usando uma fila de prioridade.
Em termos de eficiência de compressão, o algoritmo de Huffman é ótimo para compressão símbolo a símbolo, garantindo a menor representação possível quando as probabilidades dos símbolos são potências de 2.
1.4 Aplicabilidade em Big Data e Transmissão em Tempo Real
Para cenários de big data, o algoritmo de Huffman pode ser eficaz, especialmente quando lidamos com dados que têm uma distribuição de frequência de símbolos bem definida e estável. No entanto, para transmissões em tempo real, o algoritmo de Huffman pode enfrentar desafios, pois requer dois passes pelos dados: um para calcular as frequências e outro para codificar.
2. Algoritmo LZ77
2.1 Fundamentos Teóricos
O algoritmo LZ77, desenvolvido por Abraham Lempel e Jacob Ziv em 1977, é um algoritmo de compressão baseado em dicionário que utiliza uma janela deslizante para identificar e codificar sequências repetidas de dados.
2.2 Implementação
Vamos examinar uma implementação simplificada do LZ77 em Python:
def find_longest_match(data, current_position, window_size):
end_of_buffer = min(current_position + window_size, len(data))
best_length = 0
best_offset = 0
buffer = data[current_position:end_of_buffer]
for i in range(current_position - window_size, current_position):
start = max(0, i)
chunk = data[start:current_position]
for length in range(len(chunk), 0, -1):
if chunk[-length:] == buffer[:length] and length > best_length:
best_length = length
best_offset = current_position - start - length
break
return (best_offset, best_length)
def lz77_compress(data, window_size=4096, lookahead_buffer_size=16):
compressed = []
current_position = 0
while current_position < len(data):
match = find_longest_match(data, current_position, min(window_size, lookahead_buffer_size))
if match[1] > 0:
compressed.append(match)
current_position += match[1]
else:
compressed.append((0, 0, data[current_position]))
current_position += 1
return compressed
# Exemplo de uso
data = "ABCABCABCABC"
compressed = lz77_compress(data)
print("Dados comprimidos:", compressed)
2.3 Análise de Eficiência
A complexidade de tempo do LZ77 é O(n*m), onde n é o tamanho dos dados de entrada e m é o tamanho da janela de busca. Na prática, como m é geralmente fixo, a complexidade se aproxima de O(n).
O LZ77 é particularmente eficiente para dados com muitas repetições locais, como texto ou código-fonte.
2.4 Aplicabilidade em Big Data e Transmissão em Tempo Real
O LZ77 é bem adequado para cenários de big data e transmissão em tempo real devido à sua natureza de passagem única. Ele pode começar a comprimir dados assim que começam a chegar, tornando-o ideal para streams de dados contínuos.
3. Algoritmos Baseados em Dicionário
3.1 Fundamentos Teóricos
Os algoritmos baseados em dicionário, como o LZW (Lempel-Ziv-Welch), são uma evolução do LZ77. Eles mantêm um dicionário de sequências encontradas e as substituem por índices neste dicionário.
3.2 Implementação
Vamos examinar uma implementação básica do LZW em Python:
def lzw_compress(data):
dictionary = {chr(i): i for i in range(256)}
result = []
w = ""
code = 256
for c in data:
wc = w + c
if wc in dictionary:
w = wc
else:
result.append(dictionary[w])
dictionary[wc] = code
code += 1
w = c
if w:
result.append(dictionary[w])
return result
# Exemplo de uso
data = "TOBEORNOTTOBEORTOBEORNOT"
compressed = lzw_compress(data)
print("Dados comprimidos:", compressed)
3.3 Análise de Eficiência
A complexidade de tempo do LZW é O(n), onde n é o tamanho dos dados de entrada. O LZW é geralmente mais eficiente que o LZ77 em termos de velocidade de compressão, especialmente para dados com padrões repetitivos em larga escala.
3.4 Aplicabilidade em Big Data e Transmissão em Tempo Real
Os algoritmos baseados em dicionário, como o LZW, são excelentes para cenários de big data devido à sua eficiência linear. Para transmissões em tempo real, eles podem ser adaptados para usar dicionários dinâmicos que se atualizam conforme novos dados chegam.
4. Comparação e Análise
4.1 Eficiência de Compressão
Huffman: Ótimo para compressão símbolo a símbolo, mas limitado em capturar redundâncias de ordem superior.
LZ77: Eficaz em capturar redundâncias locais, ideal para dados com repetições próximas.
Algoritmos baseados em dicionário (LZW): Excelentes em capturar padrões repetitivos em larga escala.
4.2 Velocidade de Compressão/Descompressão
Huffman: Requer dois passes pelos dados, o que pode ser lento para grandes volumes.
LZ77: Compressão de passagem única, mas a busca na janela pode ser computacionalmente intensiva.
LZW: Geralmente o mais rápido dos três, com complexidade linear.
4.3 Uso de Memória
Huffman: Requer armazenamento da árvore de Huffman.
LZ77: Uso de memória limitado pelo tamanho da janela deslizante.
LZW: Pode requerer grandes dicionários, potencialmente consumindo mais memória.
4.4 Adaptabilidade a Diferentes Tipos de Dados
Huffman: Melhor para dados com distribuição de frequência estável.
LZ77: Bom para dados com redundâncias locais.
LZW: Excelente para dados com padrões repetitivos em larga escala.
5. Aplicações Práticas em Big Data e Transmissão em Tempo Real
5.1 Big Data
Para cenários de big data, a escolha do algoritmo depende da natureza dos dados e dos recursos computacionais disponíveis:
Para análise de logs ou dados textuais, o LZW pode ser uma escolha excelente devido à sua eficiência com padrões repetitivos.
Para dados científicos ou numéricos, o Huffman pode ser mais apropriado se a distribuição de valores for conhecida e estável.
O LZ77 pode ser uma boa opção para dados mistos ou quando a natureza dos dados não é bem conhecida antecipadamente.
5.2 Transmissão em Tempo Real
Para transmissões em tempo real, a velocidade de compressão e descompressão é crucial:
O LZ77 e suas variantes (como o LZSS) são frequentemente usados em protocolos de comunicação em tempo real devido à sua natureza de passagem única.
Algoritmos baseados em dicionário com dicionários adaptativos podem ser eficazes para streams de longa duração.
O Huffman adaptativo, que atualiza as frequências e a árvore em tempo real, pode ser uma opção para streams com características variáveis.
Conclusão
A escolha do algoritmo de compressão sem perdas ideal para cenários de big data e transmissão em tempo real depende de vários fatores, incluindo a natureza dos dados, os requisitos de velocidade e os recursos computacionais disponíveis.
O algoritmo de Huffman oferece compressão ótima para distribuições de símbolos conhecidas, mas pode ser menos eficiente para dados com padrões complexos. O LZ77 e suas variantes são excelentes para capturar redundâncias locais e são bem adequados para transmissões em tempo real. Os algoritmos baseados em dicionário, como o LZW, oferecem um bom equilíbrio entre eficiência de compressão e velocidade, tornando-os ideais para muitos cenários de big data.
Na prática, muitos sistemas de compressão modernos combinam elementos desses algoritmos para alcançar o melhor desempenho possível. Por exemplo, o algoritmo DEFLATE, usado no formato ZIP, combina LZ77 com codificação Huffman.
Ao projetar sistemas que lidam com grandes volumes de dados ou transmissões em tempo real, é crucial considerar cuidadosamente as características dos dados e os requisitos do sistema para escolher a abordagem de compressão mais apropriada. Além disso, é importante realizar testes comparativos com conjuntos de dados representativos para garantir que a solução escolhida atenda às necessidades específicas do projeto.