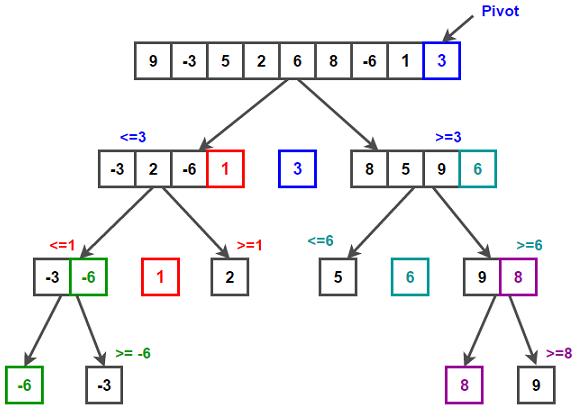
No vasto universo da ciência da computação, poucos algoritmos capturam a essência da elegância e eficiência como o Quicksort. Desenvolvido por Tony Hoare em 1960, este algoritmo de ordenação tem sido objeto de estudo, otimização e debate por décadas. Neste artigo, mergulharemos nas profundezas do Quicksort, explorando sua mecânica interna, analisando sua complexidade e discutindo otimizações avançadas que o tornam uma escolha preferida em muitas implementações de bibliotecas de ordenação.

Fundamentos do Quicksort

O Quicksort é um algoritmo de ordenação baseado na estratégia de dividir para conquistar. Sua abordagem fundamental pode ser resumida em três passos:

1. Escolha de um pivô: Seleciona um elemento do array como pivô.

2. Particionamento: Reorganiza o array de forma que elementos menores que o pivô fiquem à esquerda e os maiores à direita.

3. Recursão: Aplica o mesmo processo recursivamente nas sub-arrays à esquerda e à direita do pivô.

Vamos examinar uma implementação básica em Python:

def quicksort(arr):
    if len(arr) <= 1:
        return arr
    else:
        pivot = arr[len(arr) // 2]
        left = [x for x in arr if x < pivot]
        middle = [x for x in arr if x == pivot]
        right = [x for x in arr if x > pivot]
        return quicksort(left) + middle + quicksort(right)

Esta implementação, embora clara, não é a mais eficiente. Ela cria novas listas a cada recursão, consumindo memória adicional. Uma implementação in-place seria mais eficiente em termos de espaço:

def partition(arr, low, high):
    i = low - 1
    pivot = arr[high]
    
    for j in range(low, high):
        if arr[j] <= pivot:
            i += 1
            arr[i], arr[j] = arr[j], arr[i]
    
    arr[i + 1], arr[high] = arr[high], arr[i + 1]
    return i + 1

def quicksort_inplace(arr, low, high):
    if low < high:
        pi = partition(arr, low, high)
        quicksort_inplace(arr, low, pi - 1)
        quicksort_inplace(arr, pi + 1, high)

# Uso:
# arr = [10, 7, 8, 9, 1, 5]
# quicksort_inplace(arr, 0, len(arr) - 1)

Análise de Complexidade

A análise de complexidade do Quicksort é fascinante devido à sua natureza probabilística. Vamos examinar os casos:

Melhor Caso e Caso Médio

No melhor caso e no caso médio, o Quicksort tem uma complexidade de tempo de O(n log n). Isso ocorre quando o pivô escolhido divide o array em duas partes aproximadamente iguais a cada recursão.

A recorrência para este caso pode ser expressa como:

T(n) = 2T(n/2) + O(n)

Onde O(n) é o tempo para o particionamento. Resolvendo esta recorrência, chegamos a O(n log n).

Pior Caso

O pior caso ocorre quando o pivô escolhido é sempre o menor ou o maior elemento, resultando em uma partição altamente desequilibrada. Neste cenário, a complexidade de tempo degrada para O(n²).

A recorrência para o pior caso é:

T(n) = T(n-1) + O(n)

Que resolve para O(n²).

Otimizações Avançadas

Escolha do Pivô

A escolha do pivô é crucial para o desempenho do Quicksort. Algumas estratégias avançadas incluem:

1. Mediana de Três: Escolhe o pivô como a mediana entre o primeiro, o meio e o último elemento do array.

def median_of_three(arr, low, high):
    mid = (low + high) // 2
    if arr[low] <= arr[mid] <= arr[high] or arr[high] <= arr[mid] <= arr[low]:
        return mid
    elif arr[mid] <= arr[low] <= arr[high] or arr[high] <= arr[low] <= arr[mid]:
        return low
    else:
        return high

2. Amostragem Aleatória: Seleciona um número fixo de elementos aleatoriamente e usa sua mediana como pivô.

Particionamento de Três Vias

Para arrays com muitos elementos duplicados, o particionamento de três vias pode ser mais eficiente:

def quicksort_three_way(arr, low, high):
    if high <= low:
        return
    
    lt, i, gt = low, low + 1, high
    pivot = arr[low]
    
    while i <= gt:
        if arr[i] < pivot:
            arr[lt], arr[i] = arr[i], arr[lt]
            lt += 1
            i += 1
        elif arr[i] > pivot:
            arr[i], arr[gt] = arr[gt], arr[i]
            gt -= 1
        else:
            i += 1
    
    quicksort_three_way(arr, low, lt - 1)
    quicksort_three_way(arr, gt + 1, high)

Combinação com Insertion Sort

Para pequenos subarrays, o Insertion Sort pode ser mais eficiente. Uma otimização comum é usar Insertion Sort para subarrays menores que um certo limiar:

def insertion_sort(arr, low, high):
    for i in range(low + 1, high + 1):
        key = arr[i]
        j = i - 1
        while j >= low and arr[j] > key:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key

def optimized_quicksort(arr, low, high):
    while low < high:
        if high - low + 1 < 10:  # Limiar arbitrário
            insertion_sort(arr, low, high)
            break
        else:
            pivot = partition(arr, low, high)
            if pivot - low < high - pivot:
                optimized_quicksort(arr, low, pivot - 1)
                low = pivot + 1
            else:
                optimized_quicksort(arr, pivot + 1, high)
                high = pivot - 1

Comparação com Outros Algoritmos de Ordenação

Embora o Quicksort seja geralmente mais rápido na prática, é importante compará-lo com outros algoritmos de ordenação avançados:

1. Mergesort: Garante O(n log n) em todos os casos, mas geralmente é mais lento que o Quicksort médio devido a operações de cópia adicionais.

2. Heapsort: Também garante O(n log n) no pior caso e não requer espaço adicional, mas tem um desempenho médio inferior ao Quicksort.

3. Introsort: Uma variante híbrida que começa com Quicksort e muda para Heapsort se a profundidade da recursão ficar muito grande, garantindo O(n log n) no pior caso.

Aplicações Práticas e Considerações

O Quicksort é amplamente utilizado em bibliotecas de ordenação de várias linguagens de programação. Por exemplo, o método Arrays.sort() em Java usa uma variante do Quicksort para tipos primitivos.

Ao implementar o Quicksort em sistemas reais, considere:

1. Estabilidade: Quicksort não é estável por natureza. Se a estabilidade for necessária, considere usar Mergesort.

2. Paralelismo: O Quicksort pode ser paralelizado, especialmente em suas chamadas recursivas, tornando-o adequado para sistemas multicore.

3. Uso de Memória: Embora a versão in-place use O(log n) de espaço de pilha devido à recursão, implementações iterativas podem reduzir isso para O(1).

Conclusão

O Quicksort permanece como um dos algoritmos de ordenação mais fascinantes e práticos na ciência da computação. Sua eficiência média, combinada com otimizações inteligentes, o torna uma escolha preferida em muitas aplicações do mundo real.

Ao explorar o Quicksort, não apenas ganhamos insights sobre um algoritmo específico, mas também sobre princípios fundamentais de design de algoritmos, análise de complexidade e otimização. Esses conceitos são cruciais para qualquer programador que aspire a criar sistemas eficientes e escaláveis.

À medida que continuamos a enfrentar desafios computacionais cada vez mais complexos, algoritmos como o Quicksort nos lembram da importância de entender profundamente os fundamentos da ciência da computação. Eles nos inspiram a buscar constantemente melhorias e inovações, mesmo em conceitos aparentemente bem estabelecidos.

Powered by wisp